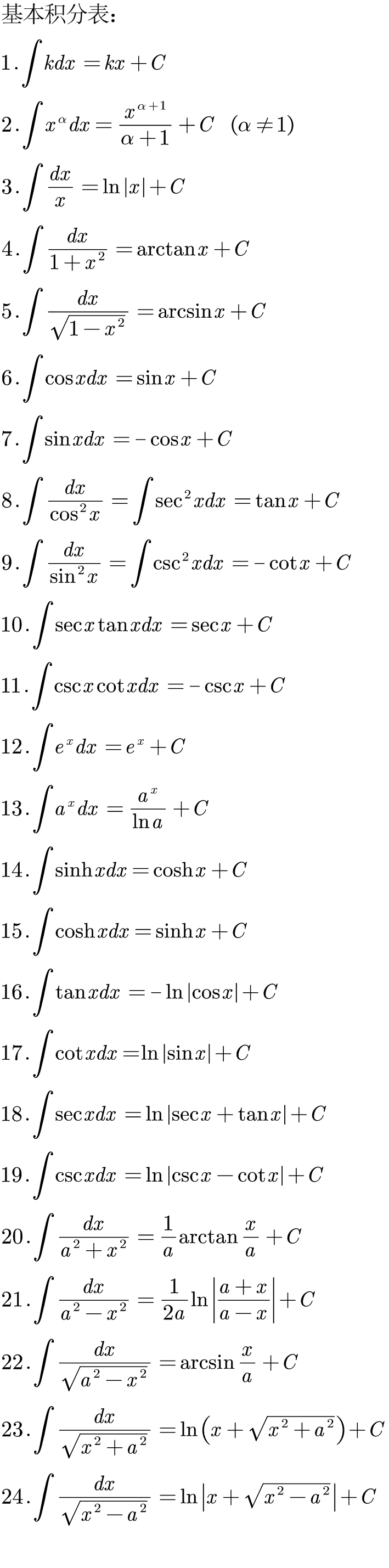高等数学期末复习
往年期末真题 提取码: f3qh
极限
函数极限
无穷小
极限的计算

重要极限
等价无穷小

洛必达
泰勒公式

数列极限
夹逼准则

连续点与间断点

零点定理与介值定理
零点定理
介值定理
导数与微分
导数概念

求导
反函数求导
复合函数求导
链式法则
隐函数求导
参数方程求导
注意高阶导数求法
高阶导数

莱布尼茨公式
微分中值定理与导数的应用
微分中值定理
泰勒公式
泰勒多项式+余项=泰勒公式
麦克劳林公式:
\[ f(x)=\sum_{k = 0}^{n}\frac{f^{(k)}(0)}{k!}x^k + R_n(x), 其中f^{(k)}(0)是f(x)在x = 0处的k阶导数,k!是k的阶乘,R_n(x)是余项。 \]
展开式:
\[ \begin{aligned} e^{x}&=\sum_{n=0}^{\infty} \frac{1}{n !} x^{n}=1+x+\frac{1}{2 !} x^{2}+\cdots \in(-\infty,+\infty) \\ \sin x&=\sum_{n=0}^{\infty} \frac{(-1)^{n}}{(2 n+1) !} x^{2 n+1}=x-\frac{1}{3 !} x^{3}+\frac{1}{5 !} x^{5}+\cdots, x \in(-\infty,+\infty) \\ \cos x&=\sum_{n=0}^{\infty} \frac{(-1)^{n}}{(2 n) !} x^{2 n}=1-\frac{1}{2 !} x^{2}+\frac{1}{4 !} x^{4}+\cdots, x \in(-\infty,+\infty) \\ \ln (1+x)&=\sum_{n=0}^{\infty} \frac{(-1)^{n}}{n+1} x^{n+1}=x-\frac{1}{2} x^{2}+\frac{1}{3} x^{3}+\cdots, x \in(-1,1] \\ \frac{1}{1-x}&=\sum_{n=0}^{\infty} x^{n}=1+x+x^{2}+x^{3}+\cdots, x \in(-1,1) \\ \frac{1}{1+x}&=\sum_{n=0}^{\infty}(-1)^{n} x^{n}=1-x+x^{2}-x^{3}+\cdots, x \in(-1,1)\\ (1+x)^{\alpha}&=1+\sum_{n=1}^{\infty} \frac{\alpha(\alpha-1) \cdots(\alpha-n+1)}{n !} x^{n}=1+\alpha x+\frac{\alpha(\alpha-1)}{2 !} x^{2}+\cdots, x \in(-1,1) \\ \arctan x&=\sum_{n=0}^{\infty} \frac{(-1)^{n}}{2 n+1} x^{2 n+1}=x-\frac{1}{3} x^{3}+\frac{1}{5} x^{5}+\cdots+ x \in[-1,1] \\ \arcsin x&=\sum_{n=0}^{\infty} \frac{(2 n) !}{4^{n}(n !)^{2}(2 n+1)} x^{2n+1}=x+\frac{1}{6} x^{3}+\frac{3}{40} x^{5}+\frac{5}{112} x^{7}+\frac{35}{1152} x^{9}+\cdots+, x \in(-1,1)\\ \tan x&=\sum_{n=1}^{\infty} \frac{B_{2 n}(-4)^{n}\left(1-4^{n}\right)}{(2 n) !} x^{2 n-1}=x+\frac{1}{3} x^{3}+\frac{2}{15} x^{5}+\frac{17}{315} x^{7}+\frac{62}{2835} x^{9}+\frac{1382}{155925} x^{11}+\frac{21844}{6081075} x^{13}+\frac{929569}{638512875} x^{15}+\cdots,x\in (-\frac{\pi}{2},\frac{\pi}{2}) \end{aligned} \]
单调性与凹凸性
极值与最值
曲率

不定积分与定积分
不定积分
部分积分不能用初等函数表示

积分公式
积分方法
分项积分
1.用分子凑分母拆成多项式的和的积分
2.三件函数变换:平方和(\(sin和cos、tan和sec\)),二倍角,积化和差
第一类换元
常用凑微分公式(举例):
\[ 1) \int f(a x+b) d x=\frac{1}{a} \int f(a x+b) d(a x+b)(a \neq 0) ;\] \[ 2) \int f(\sin x) \cos x d x=\int f(\sin x) d \sin x ;\] \[ 3) \int f(\ln x) \frac{1}{x} d x=\int f(\ln x) d \ln x ;\] \[ 4) \int f(\sqrt{x}) \frac{d x}{\sqrt{x}}=2 \int f(\sqrt{x}) d(\sqrt{x}) ;\] \[ 5) \int f(\arctan x) \frac{d x}{1+x^{2}}=\int f(\arctan x) d \arctan x .\]
第二类换元
定义:令 \(x=\psi(t)\) ,使 \(\int f(x) d x=\int f[\psi(t)] \psi^{\prime}(t) d t\) ,其中 \(x=\psi(t)\) 单调可导且 \(\psi^{\prime}(t) \neq 0\) .
三角代换 (a>0)
被积函数含 \(\sqrt{a^{2}-x^{2}}\) ,令 \(x=a \sin t, t \in\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]\) ,则 \(\sqrt{a^{2}-x^{2}}=a \cos t\) ;
被积函数含 \(\sqrt{x^{2}+a^{2}}\) ,令 \(x=a \tan t, t \in\left(-\frac{\pi}{2}, \frac{\pi}{2}\right) ,则 \sqrt{x^{2}+a^{2}}=a \sec t\) ;
被积函数含 \(\sqrt{x^{2}-a^{2}}\) ,令 \(x=a \sec t, t \in\left[0, \frac{\pi}{2}\right) \cup\left(\frac{\pi}{2}, \pi\right] ,则 \sqrt{x^{2}-a^{2}}=a|\tan t|\) ;
根式代换
被积函数含 \(\sqrt[n]{a x+b}\) ,令 \(t=\sqrt[n]{a x+b}\) ,有 \(x=\frac{1}{a}\left(t^{n}-b\right)\) .
倒代换
当被积函数分母的最高次数高于分子的最高次数时,可试用倒代换令 x= .
分部积分
表格法
口诀:反对幂指三(靠后面的放到d后面)
适用范围:幂函数与指数函数/三角函数与指数函数
有理函数积分
1.分母因式分解
2.分子待定系数法
eg.
\[ ①\frac{2x + 1}{(2x + 3)^2(2x^2 + 3x + 4)} = \frac{A_1}{2x + 3} + \frac{A_2}{(2x + 3)^2} + \frac{Bx + D}{2x^2 + 3x + 4}\] \[②\frac{2x + 6x^2}{(x - 5)(3x^2 + x + 1)^2} = \frac{A}{x - 5} + \frac{B_1x + D_1}{3x^2 + x + 1} + \frac{B_2x + D_2}{(3x^2 + x + 1)^2} \]
三角函数有理式的积分
万能代换
三角有理式积分——万能代换公式详细推导_三角有理式积分万能代换推导-CSDN博客

分段函数的积分
1.各段分别求原函数
2.注意分段点一定要连续
定积分
几何物理意义
求数列极限

变限积分
性质: \[\begin{align*} &1)\quad\text{若 }f(x)\text{ 在 }[a,b]\text{ 上可积,则函数 }F(x)=\int_{a}^{x} f(t)dt\text{ 在 }[a,b]\text{ 上连续;}\\ &2)\quad\text{若 }f(x)\text{ 在 }[a,b]\text{ 上连续,则函数 }F(x)=\int_{a}^{x} f(t)dt\text{ 在 }[a,b]\text{ 上可导,且 }F^{\prime}(x)=f(x). \end{align*}\]
对于可积:有积分值就可积(1.连续;或者2.有界且有有限个间断点)
求导:

积分方法
计算用 
证明用 
对称区间积分
1.偶倍奇邻
2.\(\quad \int_{-a}^{a} f(x)dx = \int_{0}^{a} [f(x) + f(-x)]dx.\)
可能遇到的公式: \[ \arctan x + \arctan\frac{1}{x} = \begin{cases} \frac{\pi}{2}, & x > 0 \\ -\frac{\pi}{2}, & x < 0 \end{cases} \]
换元法
积分换元必换限
华理士公式(点火公式)
\[ \text{华理士公式:}\int_{0}^{\frac{\pi}{2}}\sin^{n}xdx=\int_{0}^{\frac{\pi}{2}}\cos^{n}xdx= \begin{cases} \frac{(n - 1)!!}{n!!}\cdot\frac{\pi}{2}, & n\geq 2 \text{为正偶数},\\ \frac{(n - 1)!!}{n!!}, & n\geq 3 \text{为正奇数}. \end{cases} \]
可能的前置转换: \[\begin{align*} &\text{设 }f(x)\text{ 在区间 }[0,1]\text{ 上连续,则}\\ &1)\quad\int_{0}^{\frac{\pi}{2}} f(\sin x)dx=\int_{0}^{\frac{\pi}{2}} f(\cos x)dx;\\ &2)\quad\int_{0}^{\pi} f(\sin x)dx = 2\int_{0}^{\frac{\pi}{2}} f(\sin x)dx,\quad\int_{0}^{\pi} f(|\cos x|)dx = 2\int_{0}^{\frac{\pi}{2}} f(\cos x)dx;\\ &\text{注:在 }[0,\pi]\text{ 上 }f(\cos^{2} x), f(|\cos x|)\text{ 可以看作 }f(\sin x)\text{ ,}f(\cos x)\text{ 不可看作 }f(\sin x).\\ &3)\quad\int_{0}^{\pi} xf(\sin x)dx=\frac{\pi}{2}\int_{0}^{\pi} f(\sin x)dx;\\ &4)\quad\text{华理士公式:}\int_{0}^{\frac{\pi}{2}}\sin^{n} xdx=\int_{0}^{\frac{\pi}{2}}\cos^{n} xdx=\begin{cases} \frac{(n - 1)!!}{n!!}\cdot\frac{\pi}{2}, & n\geq 2\text{ 为正偶数},\\ \frac{(n - 1)!!}{n!!}, & n\geq 3\text{ 为正奇数}. \end{cases}\\ &5)\quad\int_{0}^{2\pi}\sin^{n} xdx=\int_{0}^{2\pi}\cos^{n} xdx=\begin{cases} 4\int_{0}^{\frac{\pi}{2}}\sin^{n} xdx, & n\text{ 为正偶数},\\ 0, & n\text{ 为正奇数}. \end{cases} \end{align*} \]
区间再现公式
反常积分(广义积分)
无穷限的反常积分
无界函数的反常积分
几何学的应用
直角坐标:

极坐标:

立体:

曲线弧长和旋转面面积:

旋转面面积可以理解为周长*弧微分的积分
物理学的应用
微分方程
可分离变量的微分方程
自变量因变量分开在等式两侧同时积分
齐次方程
定义
\[形如 \frac{dy}{dx} = f(\frac{y}{x})\ 的一阶微分方程称为齐次微分方程,简称微分方程。\]
特点
\[齐次微分方程的特点是其右端项是以\frac{y}{x}为变元的连续函数。\]\[ 例如,(x^{2}+y^{2})dx - xydy = 0是齐次微分方程,它可以转化为:\frac{dy}{dx}=\frac{x^{2}+y^{2}}{xy},即\frac{dy}{dx}=\frac{x}{y}+\frac{y}{x}。\]
方程的解
\[齐次微分方程通过\textbf{变量代换},可化为\textbf{可分离变量微分方程}来求解。\] \[ 令u = \frac{y}{x}或y = ux, \] \[其中u = u(x)是新的未知函数,对y = ux两边\textbf{求导},则有:\frac{dy}{dx} = u + x\frac{du}{dx},\] \[ 将其代入\frac{dy}{dx} = f(\frac{y}{x}),得:u + x\frac{du}{dx} = f(u),\] \[ 分离变量,得:\frac{du}{f(u) - u} = \frac{dx}{x} \] \[两边\textbf{积分},得:\int \frac{du}{f(u) - u} = \int \frac{dx}{x},\] \[ 求出积分后,再将u = \frac{y}{x}回代,便得到方程\frac{dy}{dx} = f(\frac{y}{x})的通解。\]
一阶线性微分方程
6.1.3 一阶线性方程的线性、齐次与通解公式-CSDN博客
公式:\(y = e^{-\int g(x)dx}[C + \int h(x)e^{\int g(x)dx}dx]\)
这里会有更换主元的考法
伯努利方程
这篇文章比较完全:【高等数学】伯努利方程及其求解方法_伯努利方程高数-CSDN博客

可降阶的高阶微分方程
可以连续积分型
一直积分就行了
不显含y型
不限含x型
高阶线性微分方程
利用解的结构(和线性代数的思路相似)
这里会有解的叠加原理的考法
常系数齐次线性微分方程

高阶的例题:
\(例6 求方程y^{(4)} - 2y''' + 5y'' = 0的通解.\) 解 这里的特征方程为
\[r^{4} - 2r^{3} + 5r^{2} = 0,\]
即
\[r^{2}(r^{2} - 2r + 5) = 0.\]
它的根是\(r_{1} = r_{2} = 0\)和\(r_{3,4} = 1 \pm 2\text{i}\).因此所给微分方程的通解为 \[y = C_{1} + C_{2}x + \text{e}^{x}(C_{3}\cos 2x + C_{4}\sin 2x).\]
常系数非齐次线性微分方程
微分方程第七节 常系数齐次线性微分方程 - 知乎 (zhihu.com)

附录
积分表